ProOE: Detecting Spatial Fuzzy Communities with Probabilistic Estimation

Posted on Edited on In ,
ProOE is a novel probabilistic optimal estimation method for detecting spatial fuzzy communities in urban networks. Published in IJGIS, it provides a nuanced understanding of urban structures by embracing the fuzziness of human movements.

We are excited to introduce ProOE (Probabilistic Optimal Estimation), a novel approach for detecting spatial fuzzy communities, as detailed in our recent publication in the International Journal of Geographical Information Science. This method provides a more nuanced understanding of urban structures by embracing the inherent fuzziness and heterogeneity of human movements.

You can find the full paper and the source code here:

Abstract

Urban areas comprise numerous spatial communities due to the frequent and limited range of human movements. Due to the partial spatial stochasticity of human movements, urban spatial communities are fuzzy and spatially heterogeneous. Existing spatial community detection strategies based on deterministic and globally uniform criteria fail to account for these characteristics. Therefore, this study presents a framework for detecting spatial fuzzy communities by transforming spatial fuzzy community detection into trip estimations between spatial units. We developed a probabilistic optimal estimation (ProOE) method to estimate trip volumes between spatial units by adjusting the probability of the membership of each unit in a spatial community. A trip intensity parameter was introduced for each community to adjust the estimated trip volumes. The distance decay effect (DDE) of human movement was then incorporated into the model, further improving the accuracy of community delineation for specific cities. Finally, spatial continuity guidance was incorporated into the solution algorithm, minimizing unnecessary community fragmentation. The experimental results demonstrate that ProOE outperforms existing methods, achieving an average improvement of 31.57% in accuracy while effectively capturing the ambiguity in the interplay between spatial units and communities. This study contributes to a more precise understanding of the spatial structures of cities.

A Quick Look at Existing Methods

Traditional spatial community detection methods often rely on deterministic and globally uniform criteria. However, these approaches fall short in capturing the fuzzy boundaries and spatial heterogeneity that characterize real-world urban movements.

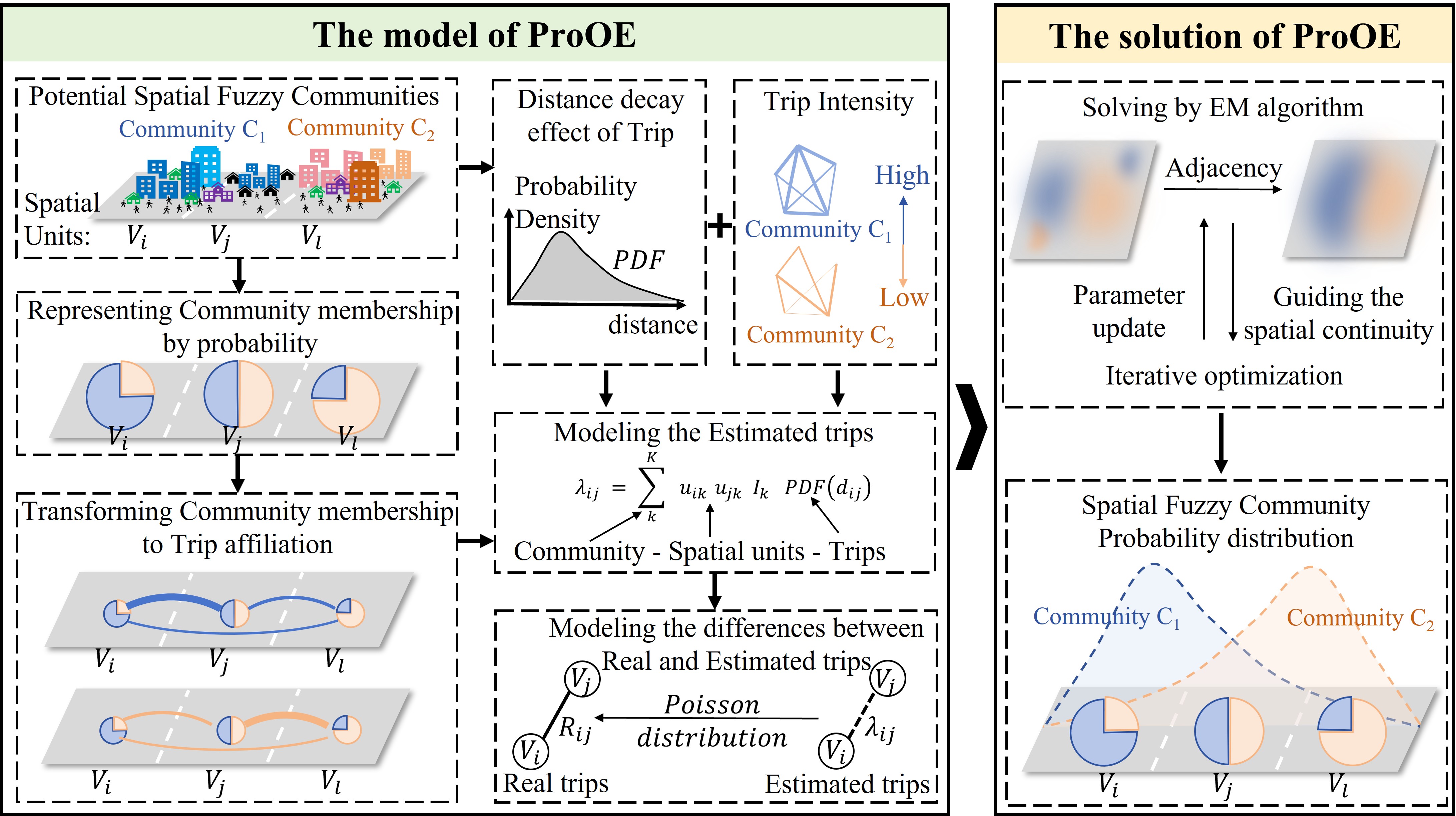
The ProOE Framework

Our ProOE method reframes the problem by transforming community detection into a trip estimation task between spatial units. The core idea is to probabilistically estimate trip volumes by iteratively adjusting the membership probabilities of each spatial unit to every community.

The framework is illustrated below, showing how ProOE integrates spatial constraints and probabilistic estimation to delineate fuzzy communities.

Figure 1: Framework of the proposed ProOE.

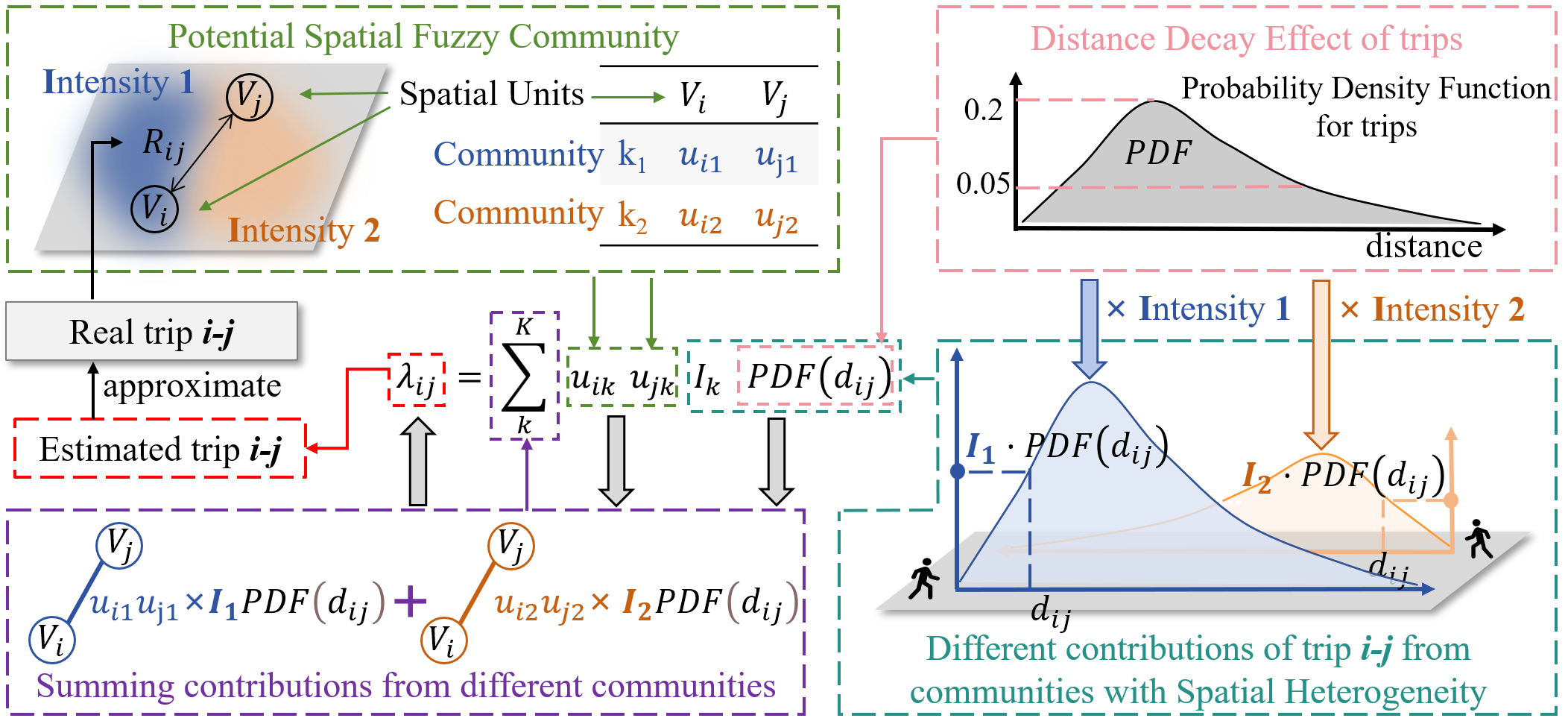
The core idea of the model is further detailed in the following illustration, which visualizes how membership probabilities are optimized.

Figure 2: Illustration of the core idea of the model.

Key Results: Simulated & Real-World Data

To validate the effectiveness of ProOE, we conducted experiments on both simulated and real-world datasets.

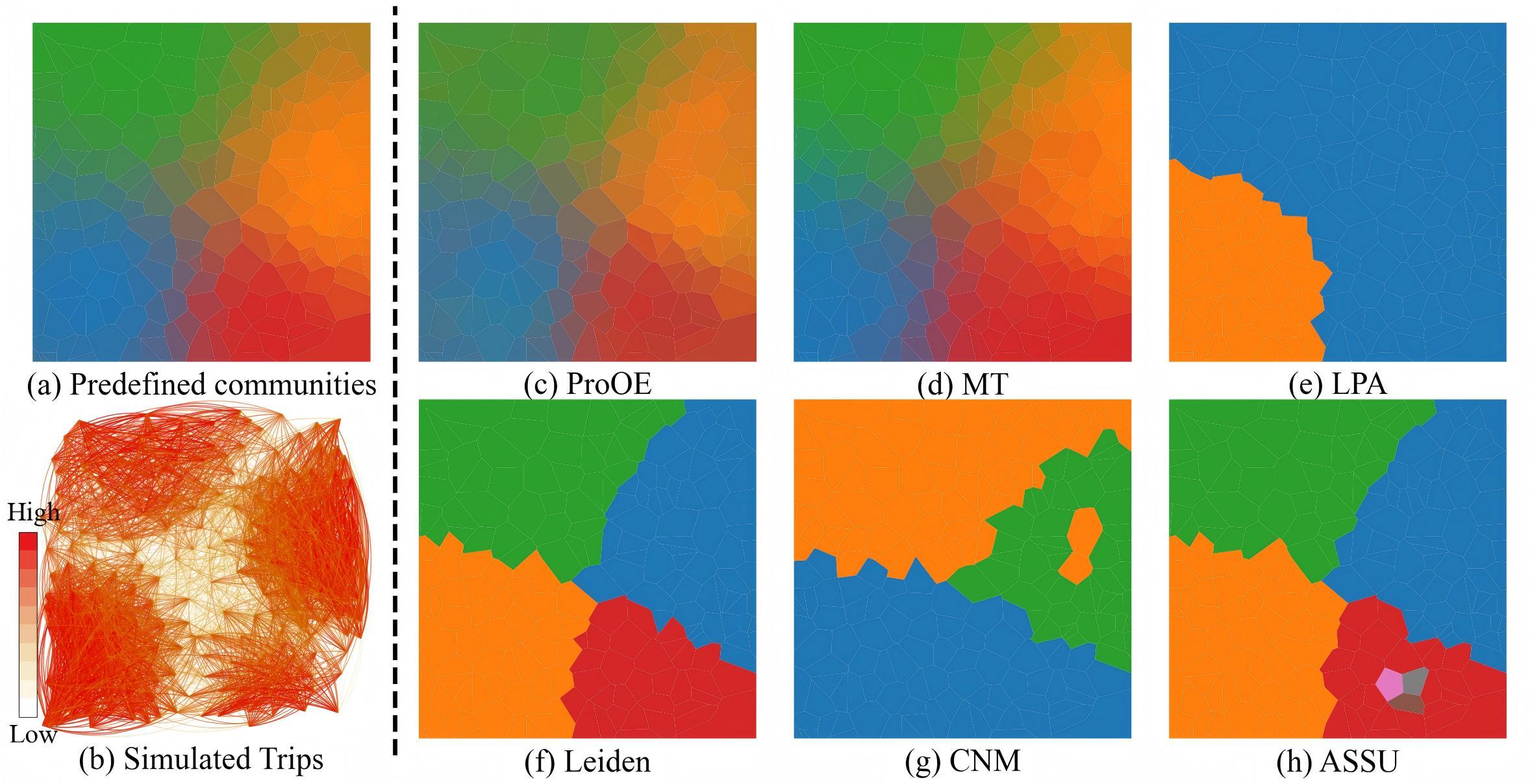
1. Performance on Simulated Datasets

We first designed three distinct simulated datasets to rigorously test the model’s ability to handle key spatial characteristics: continuity, fuzziness, and heterogeneity.

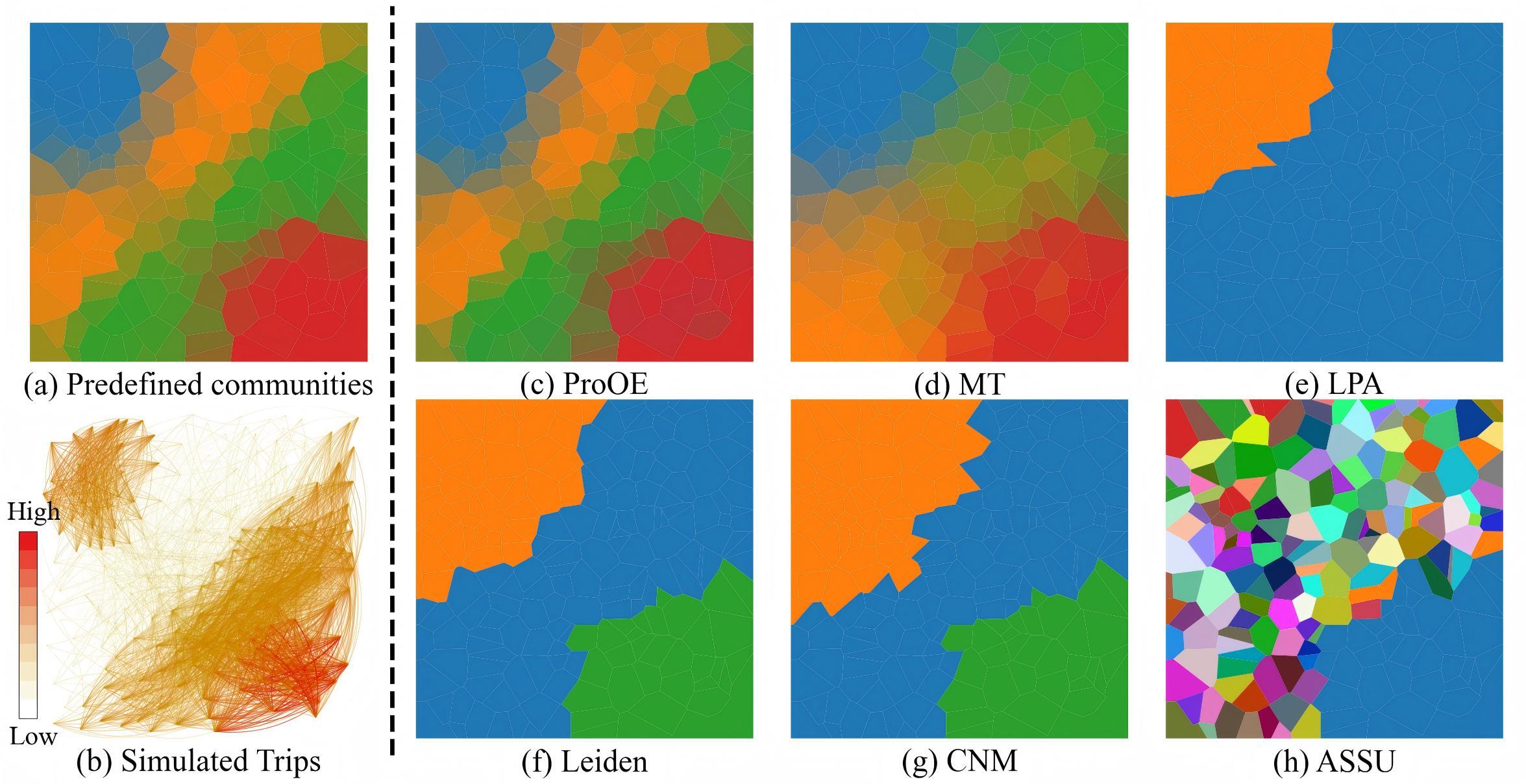
Figure 3. Simulation experiment for spatial heterogeneity. (a) and (b) display the simulated data: (a) predefined communities and (b) simulated trips. (c)–(h) Show the spatial community detection results from six different methods applied to this dataset: (c) ProOE, (d) MT, (e) LPA, (f) Leiden, (g) CNM and (h) ASSU.

The results of various community detection methods on these datasets are visualized below. It is clear that traditional methods struggle to correctly identify community structures, especially in the presence of fuzzy boundaries and varied internal densities.

Figure 4. Simulation experiment for fuzziness. (a) and (b) display the simulated data: (a) predefined communities and (b) simulated trips. (c)–(h) Show the spatial community detection results from six different methods applied to this dataset: (c) ProOE, (d) MT, (e) LPA, (f) Leiden, (g) CNM and (h) ASSU.

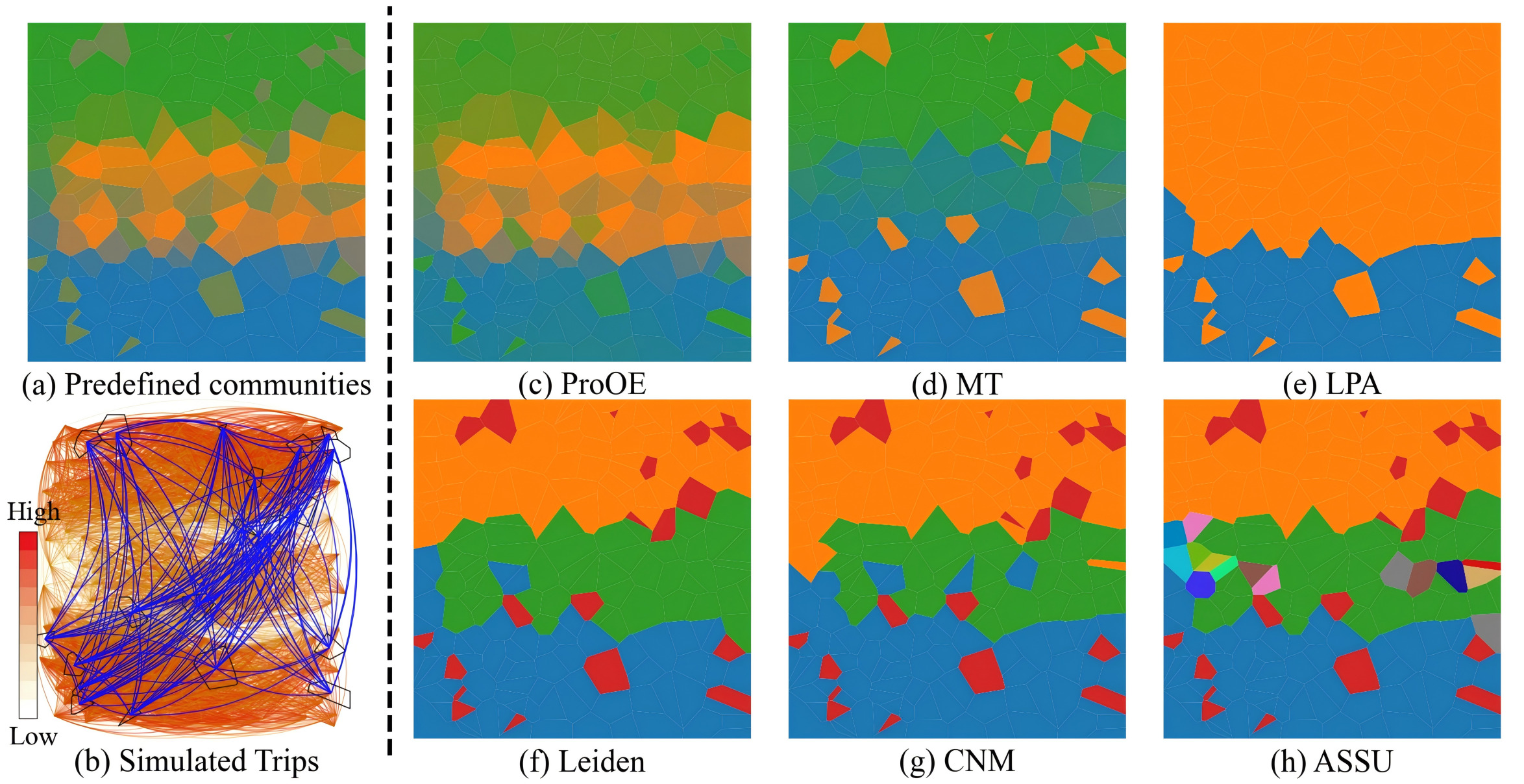
Figure 5. Simulation experiment for continuity. (a) and (b) Display the simulated data: (a) Predefined communities and (b) simulated trips, blue indicates abnormally high values. (c)–(h) Show the spatial community detection results from six different methods applied to this dataset: (c) ProOE, (d) MT, (e) LPA, (f) Leiden, (g) CNM and (h) ASSU.

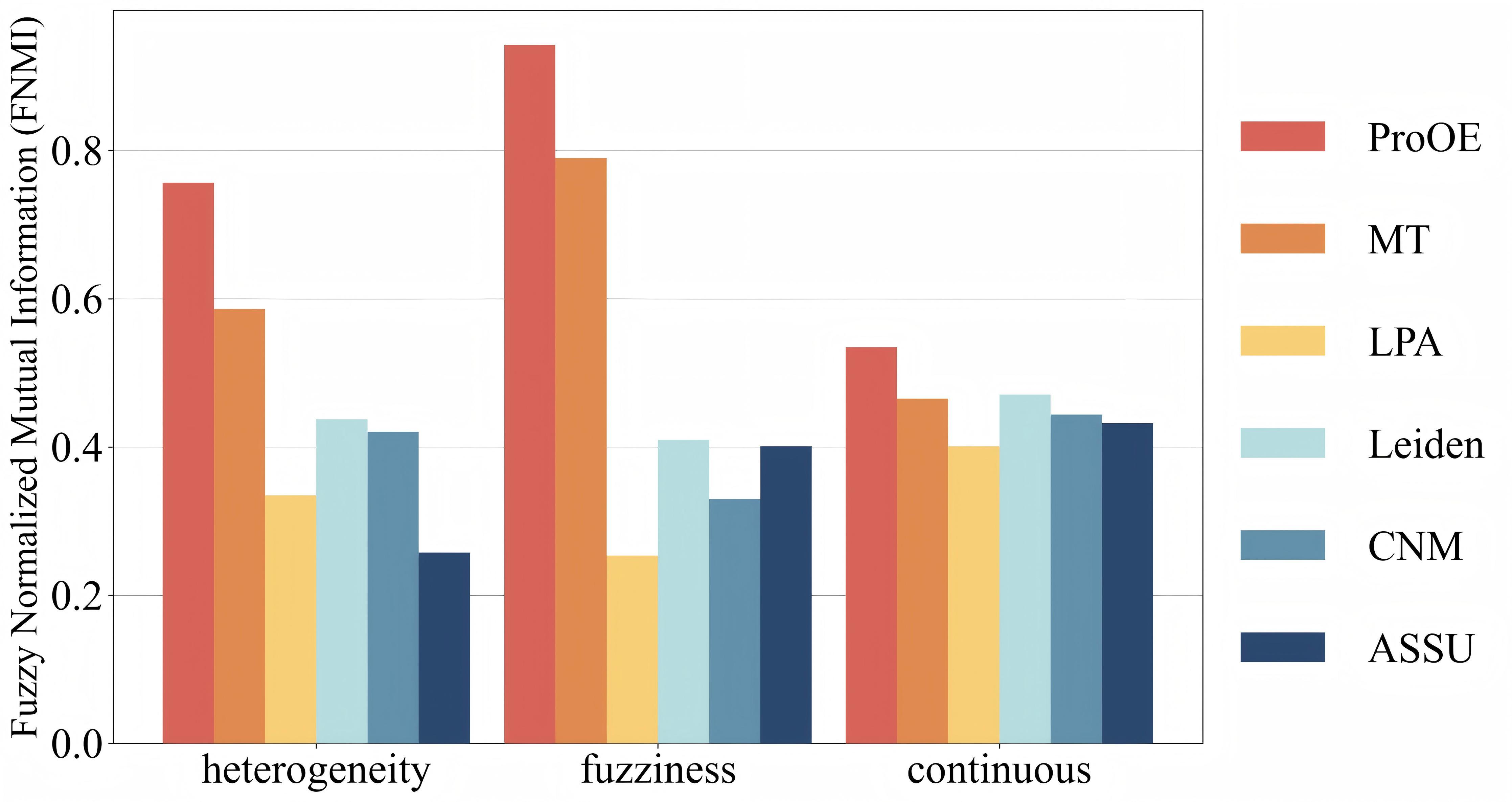
To quantify this, we used the Fuzzy Normalized Mutual Information (FNMI) metric, which measures the similarity between the detected fuzzy communities and the ground truth. A higher FNMI value indicates better accuracy. As shown below, ProOE consistently outperforms other state-of-the-art methods across all three datasets.

Figure 6. FNMI values of three simulated datasets for different methods.

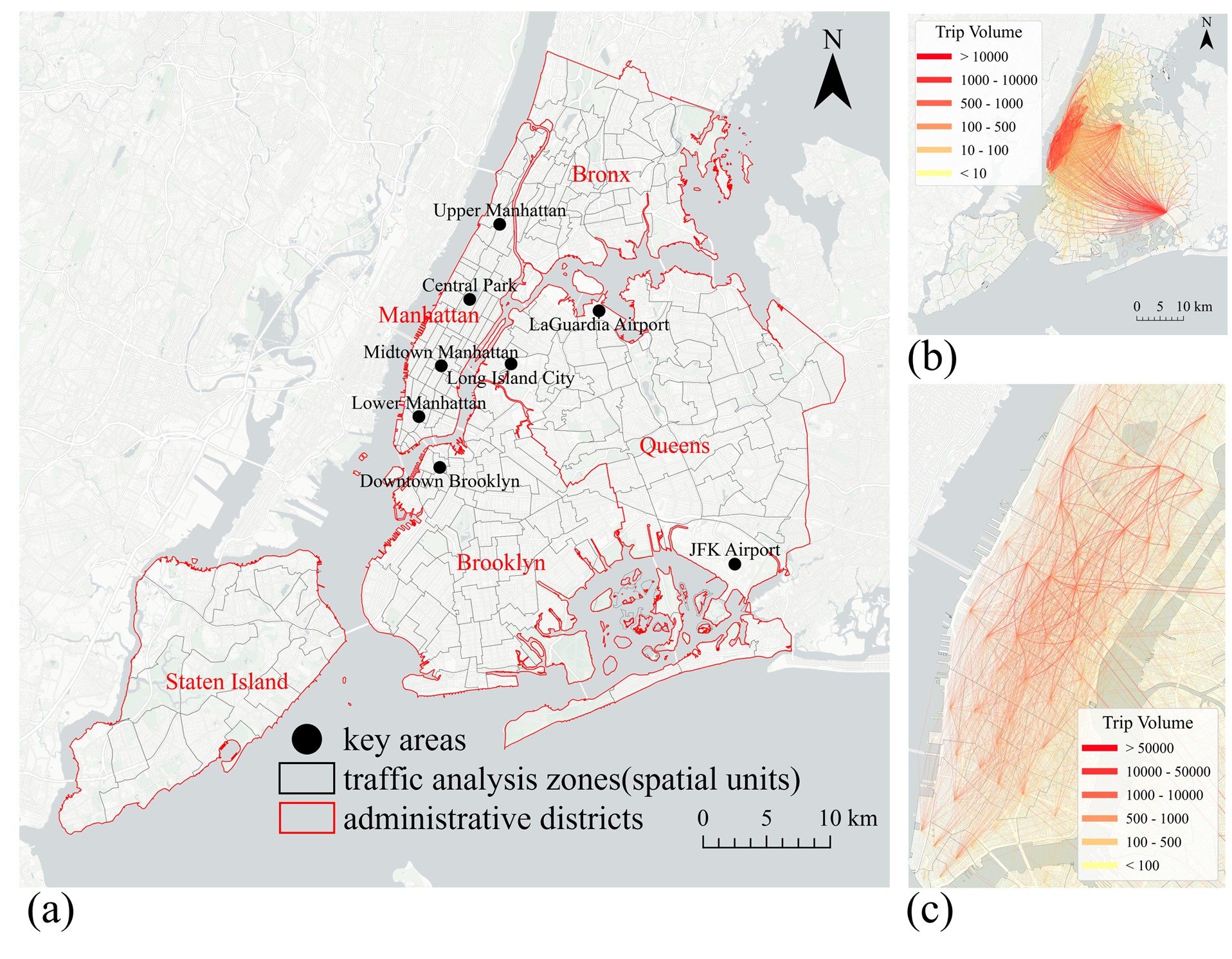
2. Case Study: New York City Taxi Trips

We then applied ProOE to a real-world dataset of New York City taxi trips to explore urban mobility patterns. The study area focuses on Manhattan, a hub of intense and complex human movement.

Figure 7: Overview of the study area and data. (a) The research area. (b) Trip data for NYC. (c) Trip data for Manhattan.

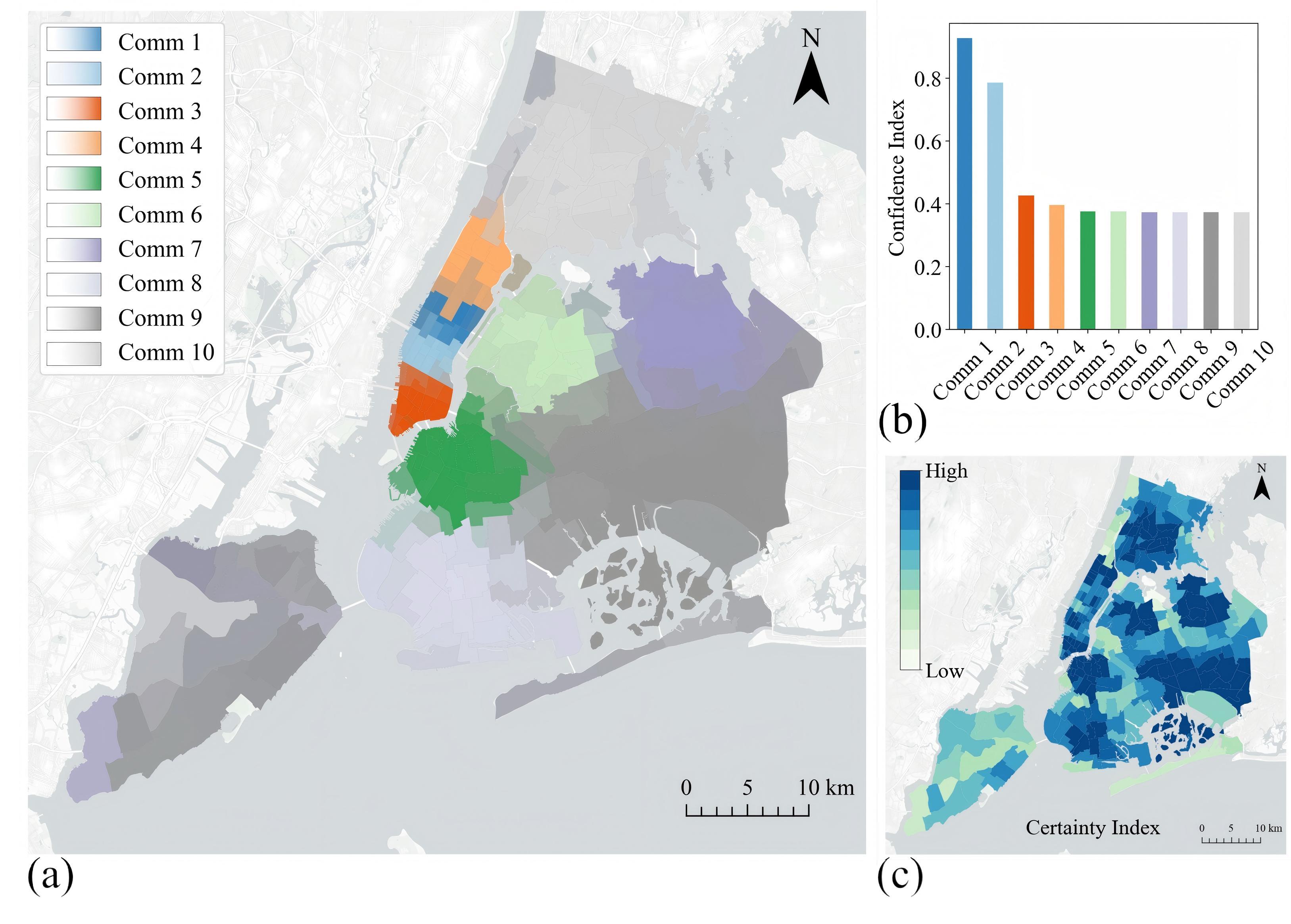
The final community structure detected by ProOE reveals a clear and meaningful division of Manhattan. The detected communities correspond well with known functional zones, such as Midtown, Upper East Side, and the financial district in Lower Manhattan. The fuzzy boundaries between these communities highlight the transitional zones where urban functions blend.

Figure 8: Detection result based on our method. (a) Spatial fuzzy community. The colors represent different communities, and the opacity indicates the membership certainty of each spatial unit.. (b) Confidence Index (ConI). (c) Certainty Index (CerI).

Demonstration Video

Check out this video demonstrating the evolution of spatial fuzzy communities in New York City, generated using the ProOE method.

This work offers a powerful new lens for urban planners, geographers, and data scientists to analyze and understand the intricate spatial fabric of our cities. We welcome you to explore the code, run the demos, and contribute to this exciting area of research!