matplotlib绘制三维散点图，并添加包围椭球及各维度核密度

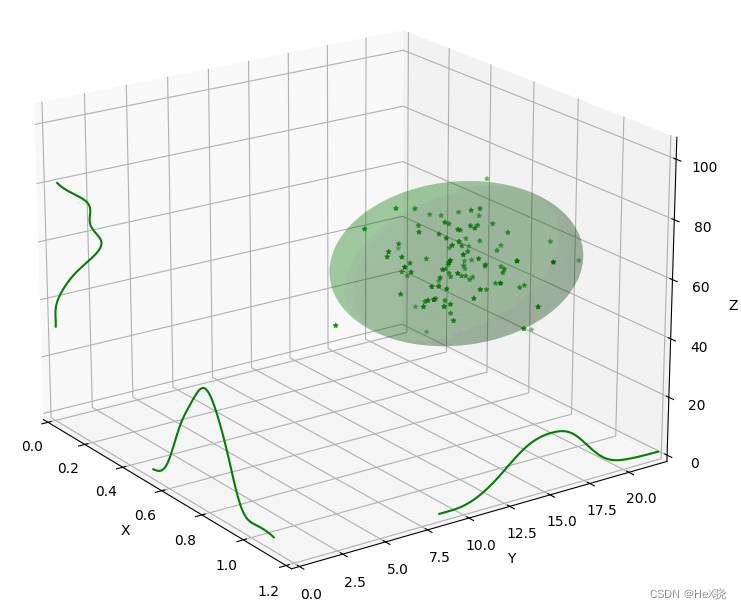
背景

我们在绘制三维散点时经常需要在一张图中描述：1.散点在空间中的分布状态；2.散点在空间不同维度的分布情况。
下面介绍一种：通过椭球描述散点在空间中的分布状态，并通过核密度曲线描述散点在空间不同维度的分布情况的方法。

实现

导入必要的库，数据准备

1
2
3
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gaussian_kde  # 导入高斯核函数

创建3D图

1
2
ax = plt.figure().add_subplot(projection='3d')
data=[]

随机生成data

定义一个函数来生成数据

1
2
3
4
5
def generate_data(mean, std_dev):
    return np.random.normal(mean, std_dev, 100)
data.append(generate_data(0.8, 0.1))
data.append(generate_data(15, 2))
data.append(generate_data(60, 10))

显示散点图的包围椭球

matplotlib中需要构造点阵以显示面，因此我们需要首先生成椭球面的XYZ坐标，然后绘制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def draw_ellipsoid(ax, data, color):
    # 计算椭球的中心
    center = np.mean(data, axis=1)

    # 计算椭球的半径
    radius = 0.5 * (np.max(data, axis=1) - np.min(data, axis=1))

    # 生成椭球的表面点
    u = np.linspace(0, 2 * np.pi, 100)
    v = np.linspace(0, np.pi, 100)
    x = center[0] + radius[0] * np.outer(np.cos(u), np.sin(v))
    y = center[1] + radius[1] * np.outer(np.sin(u), np.sin(v))
    z = center[2] + radius[2] * np.outer(np.ones(np.size(u)), np.cos(v))

    # 绘制椭球
    ax.plot_surface(x, y, z, color=color, alpha=0.2)

显示散点在空间不同维度的分布情况

matplotlib的官网实例中提到，可以采用zdir 字段实现2D内容在3D图上的绘制，这里实际上可以简单将zdir设置为2D图中“缺失的”那个维度，如下所示

在X-Z平面上绘制核密度估计图

1
2
3
4
5
def draw_kde3d_X2XZ(ax, data,  color):
    kde = gaussian_kde(data)
    xs = np.linspace(np.min(data), np.max(data), 100)
    ys = kde(xs)
    ax.plot(xs, ys*10, zs=0, zdir='y', color=color)

在Y-Z平面上绘制核密度估计图

1
2
3
4
5
def draw_kde3d_Y2YZ(ax, data,  color):
    kde = gaussian_kde(data)
    xs = np.linspace(np.min(data), np.max(data), 100)
    ys = kde(xs)
    ax.plot(xs,ys*100,  zs=[1.2 for _ in range(len(data))], zdir='x', color=color)

在Z-Y平面上绘制核密度估计图

1
2
3
4
5
def draw_kde3d_Z2ZY(ax, data,  color):
    kde = gaussian_kde(data)
    xs = np.linspace(np.min(data), np.max(data), 100)
    ys = kde(xs)
    ax.plot(ys*80,xs,  zs=0, zdir='x', color=color)

其实这里zdir其实就是与要绘制的平面相垂直的坐标轴，zdir在这里起到“临时更换坐标轴”的作用。

全部代码

1
2
3
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gaussian_kde

创建3D图

1
2
ax = plt.figure().add_subplot(projection='3d')
data=[]

随机生成data

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def generate_data(mean, std_dev):
    return np.random.normal(mean, std_dev, 100)
data.append(generate_data(0.8, 0.1))
data.append(generate_data(15, 2))
data.append(generate_data(60, 10))

def draw_ellipsoid(ax, data, color):
    # 计算椭球的中心
    center = np.mean(data, axis=1)
    # 计算椭球的半径
    radius = 0.5 * (np.max(data, axis=1) - np.min(data, axis=1))
    # 生成椭球的表面点
    u = np.linspace(0, 2 * np.pi, 100)
    v = np.linspace(0, np.pi, 100)
    x = center[0] + radius[0] * np.outer(np.cos(u), np.sin(v))
    y = center[1] + radius[1] * np.outer(np.sin(u), np.sin(v))
    z = center[2] + radius[2] * np.outer(np.ones(np.size(u)), np.cos(v))
    # 绘制椭球
    ax.plot_surface(x, y, z, color=color, alpha=0.2)

在X-Z平面上绘制核密度估计图

1
2
3
4
5
def draw_kde3d_X2XZ(ax, data,  color):
    kde = gaussian_kde(data)
    xs = np.linspace(np.min(data), np.max(data), 100)
    ys = kde(xs)
    ax.plot(xs, ys*10, zs=0, zdir='y', color=color)

在Y-Z平面上绘制核密度估计图

1
2
3
4
5
def draw_kde3d_Y2YZ(ax, data,  color):
    kde = gaussian_kde(data)
    xs = np.linspace(np.min(data), np.max(data), 100)
    ys = kde(xs)
    ax.plot(xs,ys*100,  zs=[1.2 for _ in range(len(data))], zdir='x', color=color)

在Z-Y平面上绘制核密度估计图

1
2
3
4
5
def draw_kde3d_Z2ZY(ax, data,  color):
    kde = gaussian_kde(data)
    xs = np.linspace(np.min(data), np.max(data), 100)
    ys = kde(xs)
    ax.plot(ys*80,xs,  zs=0, zdir='x', color=color)
1
xyzlims=(0, 1.2, 0, 22, 0, 105)

绘制散点图
ax.scatter(data[0], data[1], data[2], c=’g’, marker=’*’, s=10, label=’data’)

绘制椭球

1
draw_ellipsoid(ax, data, 'g')

绘制X轴方向的核密度估计

1
draw_kde3d_X2XZ(ax, data[0], 'g')

绘制Y轴方向的核密度估计

1
draw_kde3d_Y2YZ(ax, data[1], 'g')

绘制Z轴方向的核密度估计

1
2
3
4
5
draw_kde3d_Z2ZY(ax, data[2], 'g')
ax.set(xlim=(0, 1.2), ylim=(0, 22), zlim=(0, 105))
Set zoom and angle view
ax.view_init(20, -35, 0)
ax.set_box_aspect(None, zoom=1)

设置坐标轴的网格线颜色

1
2
3
4
5
6
7
ax.xaxis.pane.set_edgecolor((1.0, 1.0, 1.0, 0.0))
ax.yaxis.pane.set_edgecolor((1.0, 1.0, 1.0, 0.0))
ax.zaxis.pane.set_edgecolor((1.0, 1.0, 1.0, 0.0))
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

实现效果

效果图

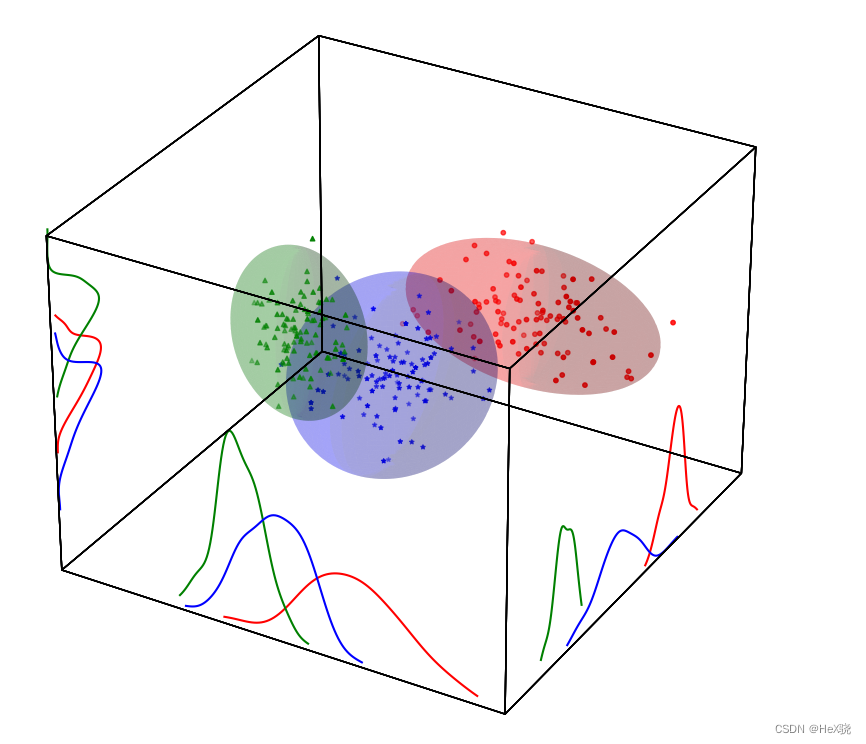
一点小改进

有些时候，我们可能有多种数据需要进行比较。这时，坐标系、网格等元素会对我们的展示造成干扰。因此，这里可以关闭这些内容的显示，并使用立方体表示三维空间。

1
2
3
4
5
6
def showbox(data,ax):  
    x, y, z = 0,0,0  #盒子坐标
    dx, dy, dz = data  #盒子长、宽、高
    ax.bar3d(x, y, z, dx, dy, dz, color="green",zsort='average',edgecolor='black',linewidth=1,alpha=0)

···其他代码···

设置坐标轴的背景颜色

1
2
3
ax.xaxis.pane.fill = False
ax.yaxis.pane.fill = False
ax.zaxis.pane.fill = False

设置坐标轴不可见

1
2
ax.axis('off')
ax.grid(False)

设置坐标轴的网格线颜色

1
2
3
ax.xaxis.pane.set_edgecolor((1.0, 1.0, 1.0, 0.0))
ax.yaxis.pane.set_edgecolor((1.0, 1.0, 1.0, 0.0))
ax.zaxis.pane.set_edgecolor((1.0, 1.0, 1.0, 0.0))

关闭坐标轴的刻度

1
2
3
4
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
box = (1.2,22,105)

显示立方体

1
2
3
4
5
showbox(box,ax)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

最终效果

最终效果

technique
#plot #python
matplotlib绘制三维散点图，并添加包围椭球及各维度核密度
https://hexiao2001.github.io/2024/12/02/matplotlib绘制三维散点图/
Author
He Xiao
Posted on
December 2, 2024
Licensed under